动态规划算法入门

【摘要】

前言

说来惭愧，大学期间对算法并不是很重视，对算法的研究也就是大二获得过省级三等奖的蓝桥杯。但是没有对算法进行系统的刷题练习，所以有些类型的算法也没有接触到。可是一般稍微大一点的互联网科技公司都会要求掌握基本的算法。这其中一定包括动态规划算法，这种算法和其他算法还有一定的区别：题目类型多、没有固定模板、难度偏高。对于没有接触过的人很难有什么思路。所以我打算单独写一篇文章来记录DP算法。

动态规划

什么是动态规划？

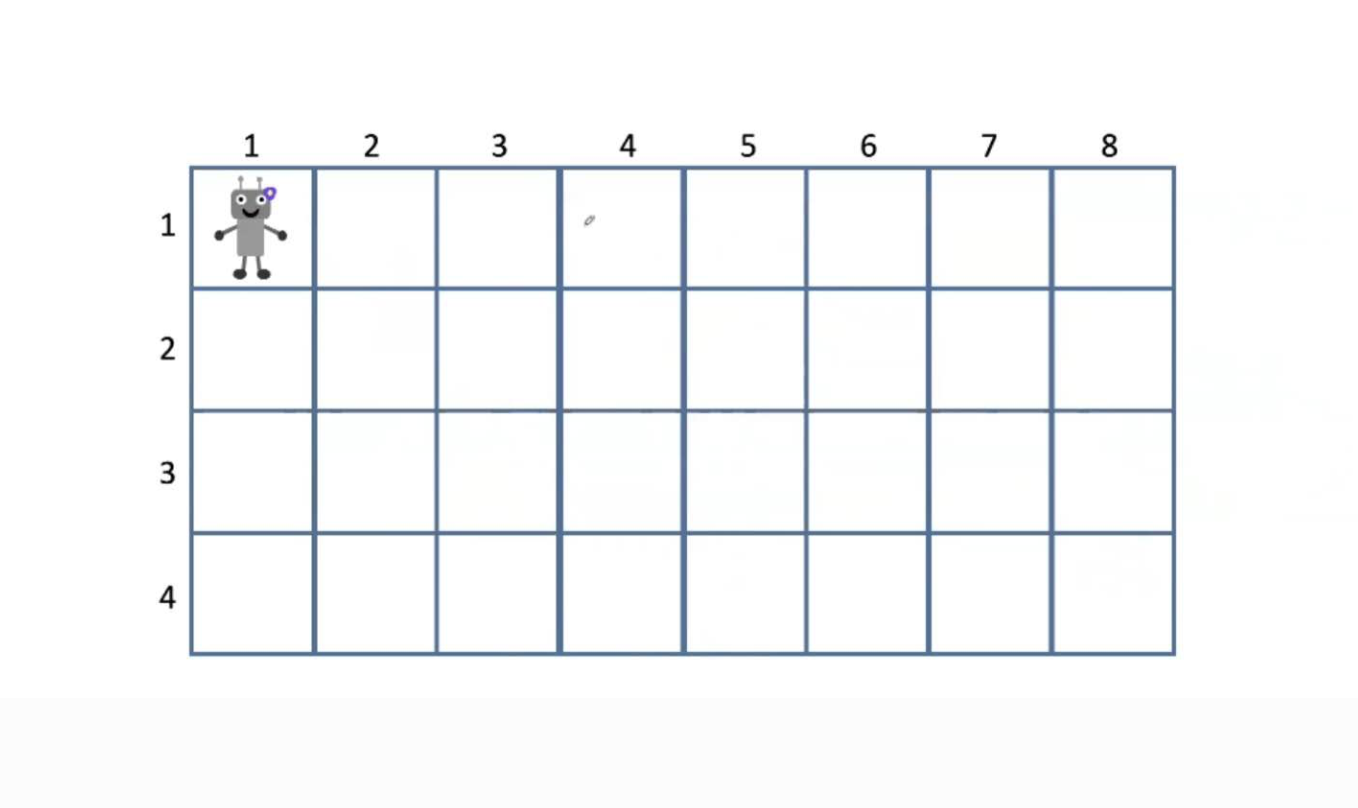
给定一个矩形网格，一个机器人从左上角出发，每次可以向下或向右走一步。

题A：求有多少种方式走到右下角。

题B：输出所有走到右下角的路径。

动态规划题目特点

• 计数

  有多少种方式走到右下角

  有多少种方式选出k个数使得和是Sum

• 求最大值最小值

  从左上角走到右下角路径的最大数字和

  最长上升子序列长度

• 求存在性

  取石子游戏，先手是否必胜

  能不能选出k个数使得和是Sum

牛刀小试

换硬币问题

题目描述

给出不同面额的硬币以及一个总金额. 写一个方法来计算给出的总金额可以换取的最少的硬币数量. 如果已有硬币的任意组合均无法与总金额面额相等, 那么返回 -1.

你可以假设每种硬币均有无数个
总金额不会超过10000
硬币的种类数不会超过500, 每种硬币的面额不会超过100

样例1
输入：
[1, 2, 5]
11
输出： 3
解释： 11 = 5 + 5 + 1

样例2
输入： 
[2]
3
输出： -1

动态规划组成部分

动态规划组成部分一：确定状态

• 状态在动态规划中的作用属于定海神针

• 简单的说，解动态规划的时候需要开一个数组，数组的每个元素f[i]或者f[i][j]代表什么？——类似于解数学题中,X,Y,Z代表什么？

• 确定状态需要两个意识：

  • 最后一步
  • 子问题

最后一步

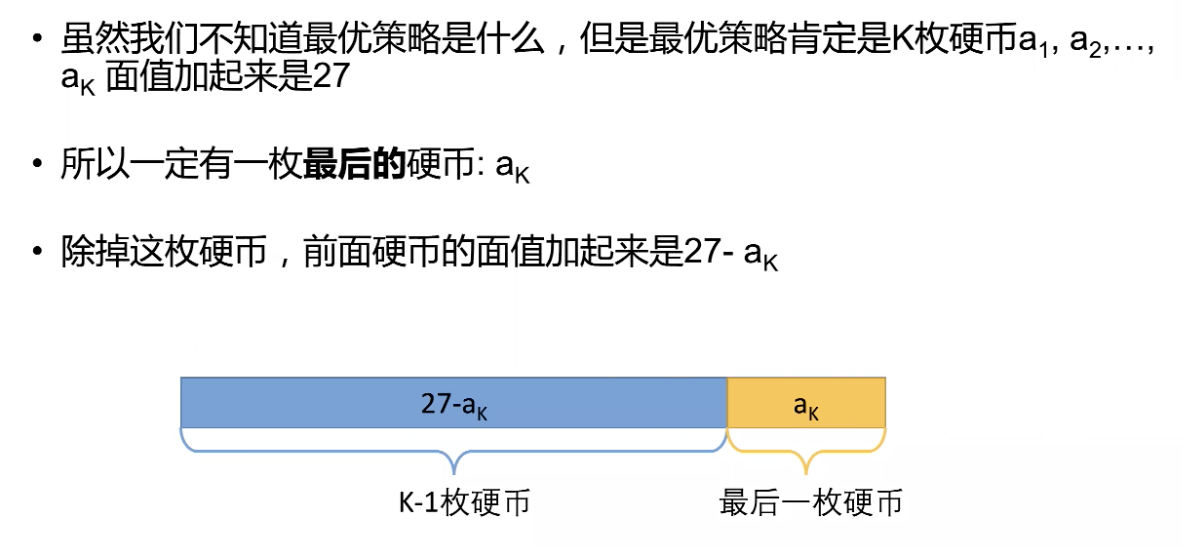
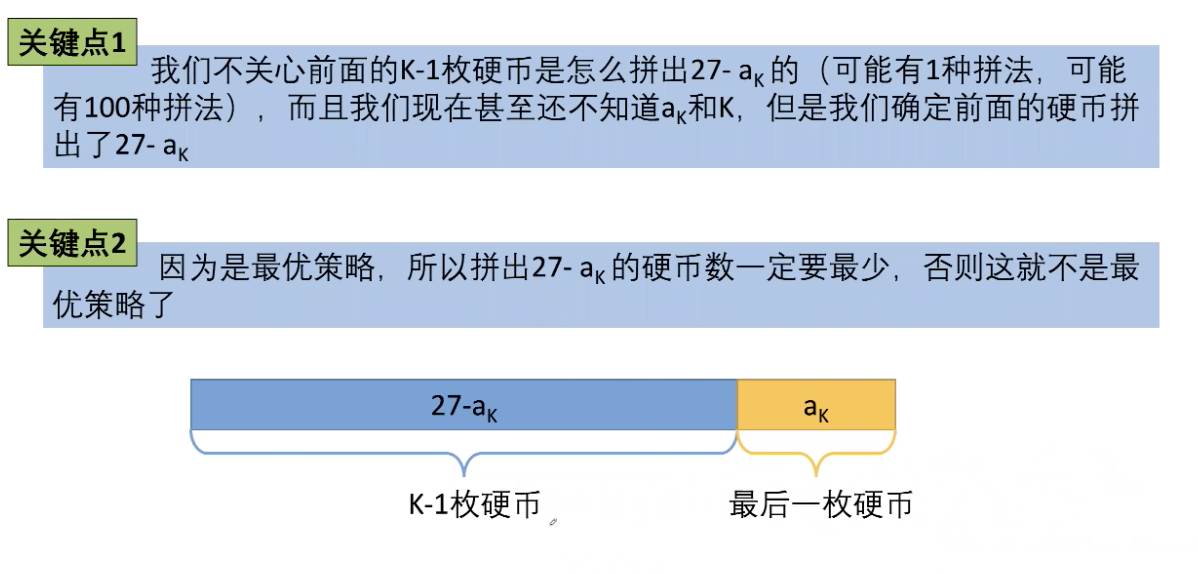
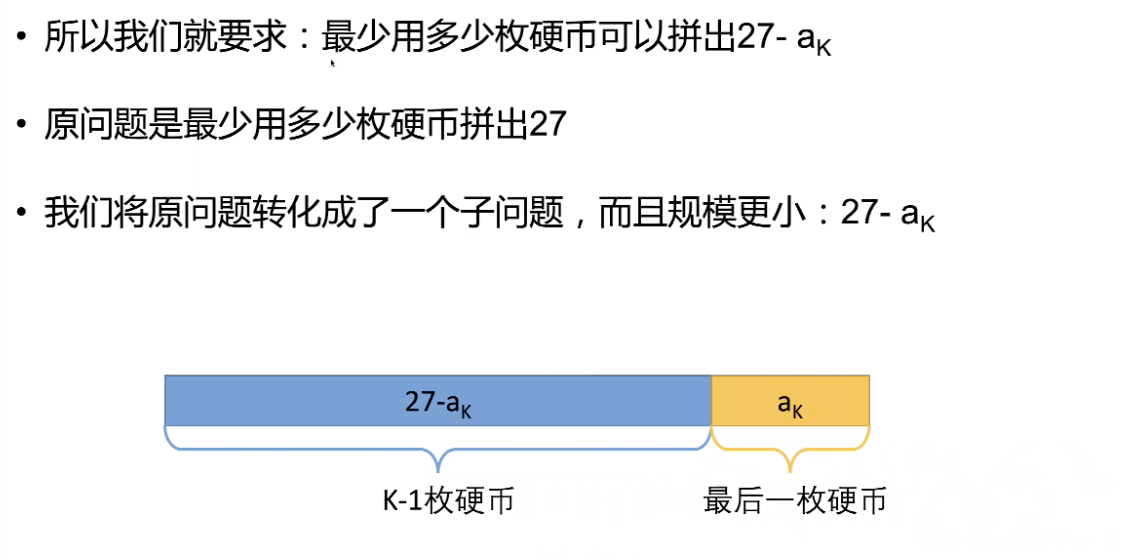
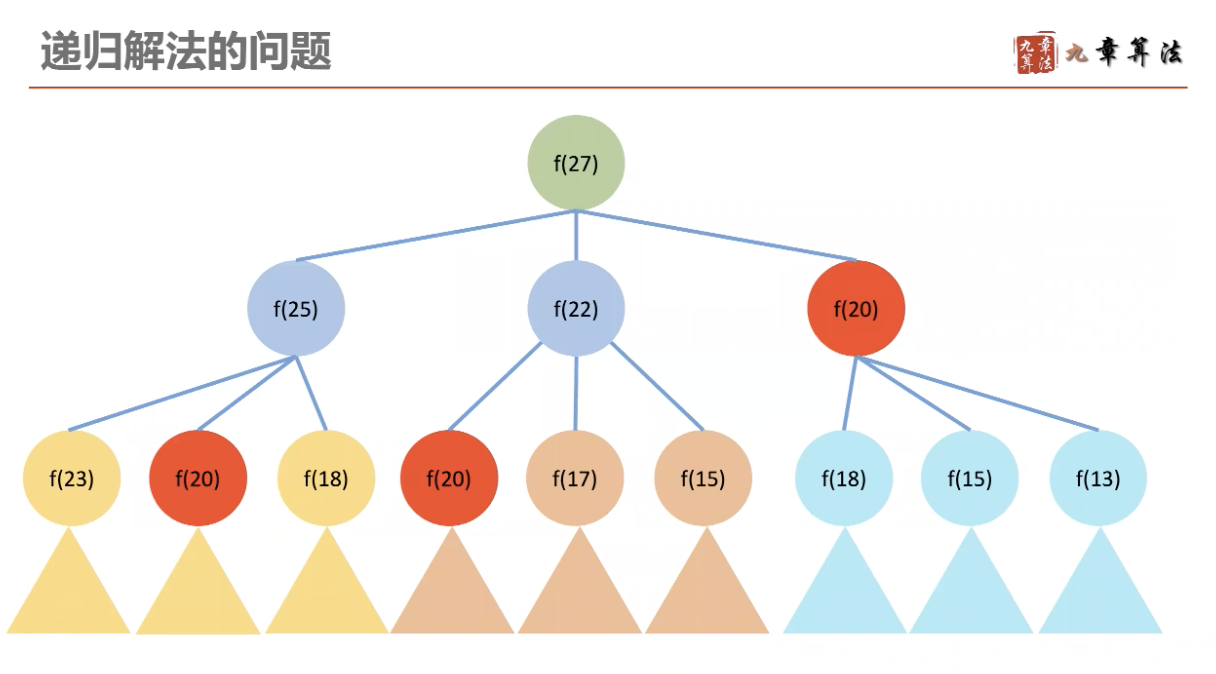
动态规划组成部分二：

动态规划组成部分三：

动态规划组成部分四：

小结

• 求最值型动态规划
• 动态规划组成部分
  • 确定状态
    • 最后一步（最优策略中使用的最后一枚硬币a_k）
    • 化为子问题（最少的硬币拼出更小的面值27-a_k）
  • 转移方程
    • f[X] = min{f[X-2]+1,f[X-5]+1,f[X-7]+1}
  • 初始条件和边界情况
    • f[0] = 0,如果不能拼出Y，f[X]=正无穷
  • 计算顺序
    • f[0],f[1],f[2]……
• 消除冗余，加速计算

不同的路径

有一个机器人的位于一个 m × n 个网格左上角。
机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。
问有多少条不同的路径？

n和m均不超过100
且答案保证在32位整数可表示范围内。

样例
Example 1:
Input: n = 1, m = 3
Output: 1	
Explanation: Only one path to target position.

Example 2:
Input:  n = 3, m = 3
Output: 6	
Explanation:
	D : Down
	R : Right
	1) DDRR
	2) DRDR
	3) DRRD
	4) RRDD
	5) RDRD
	6) RDDR

跳跃游戏

给出一个非负整数数组，你最初定位在数组的第一个位置。　　　
数组中的每个元素代表你在那个位置可以跳跃的最大长度。　　　　
判断你是否能到达数组的最后一个位置。

数组A的长度不超过5000，每个元素的大小不超过5000

样例 1
输入 : [2,3,1,1,4]
输出 : true

样例 2
输入 : [3,2,1,0,4]
输出 : false

乘积最大子序列问题

找出一个序列中乘积最大的连续子序列（至少包含一个数）。

数组长度不超过20000
乘积最大的子序列的积，小于2147483647

样例 1:
输入:[2,3,-2,4]
输出:6

样例 2:
输入:[-1,2,4,1]
输出:8

结束语

bye~